Cryptography, the science of secure communication, serves as the bedrock for safeguarding this information from prying eyes. In an era marked by the ubiquitous presence of digital data, the need to secure sensitive information has never been more critical. Whether it’s personal emails, financial transactions, or confidential business communications, the threat of data breaches looms large. In this comprehensive guide, we delve into the essential concepts of cryptography, empowering you with the knowledge to protect your data effectively of cryptography .

Understanding Cryptography:

At its core, cryptography revolves around the art of transforming plaintext into ciphertext through the use of algorithms and keys. This transformation ensures that even if intercepted, the data remains unintelligible to unauthorized parties. The fundamental components of cryptography include encryption, decryption, and key management of cryptography .

Encryption:

Encryption is the process of converting plaintext into ciphertext using an encryption algorithm and a cryptographic key. There are two primary types of encryption: symmetric and asymmetric. Symmetric encryption utilizes a single key for both encryption and decryption, making it efficient for bulk data encryption. On the other hand, asymmetric encryption employs a pair of keys – public and private – for encryption and decryption, offering enhanced security but with increased computational overhead.

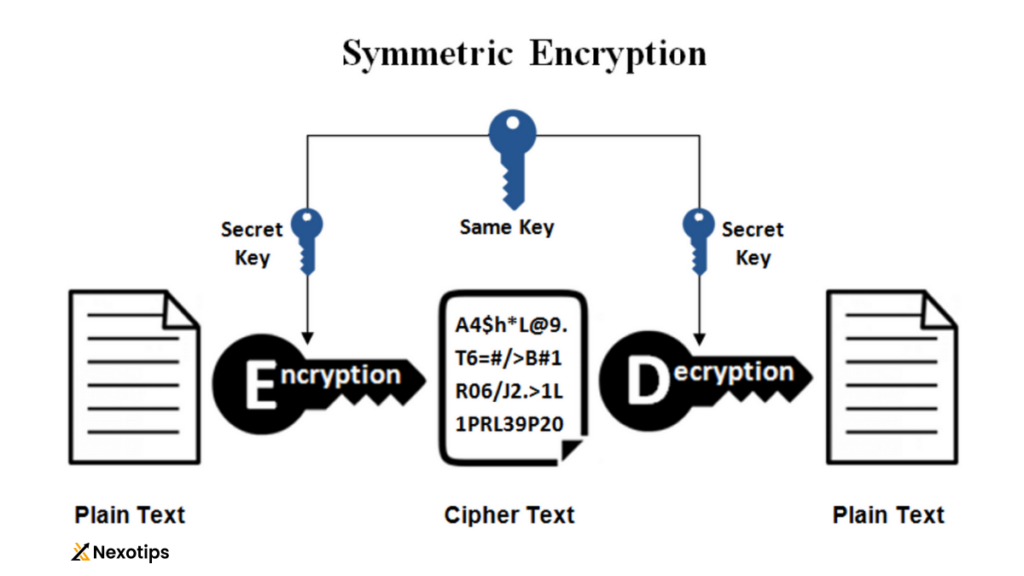
Decryption:

Decryption is the reverse process of encryption, wherein ciphertext is transformed back into plaintext using the appropriate decryption algorithm and key. This process allows authorized recipients to access the original message securely.

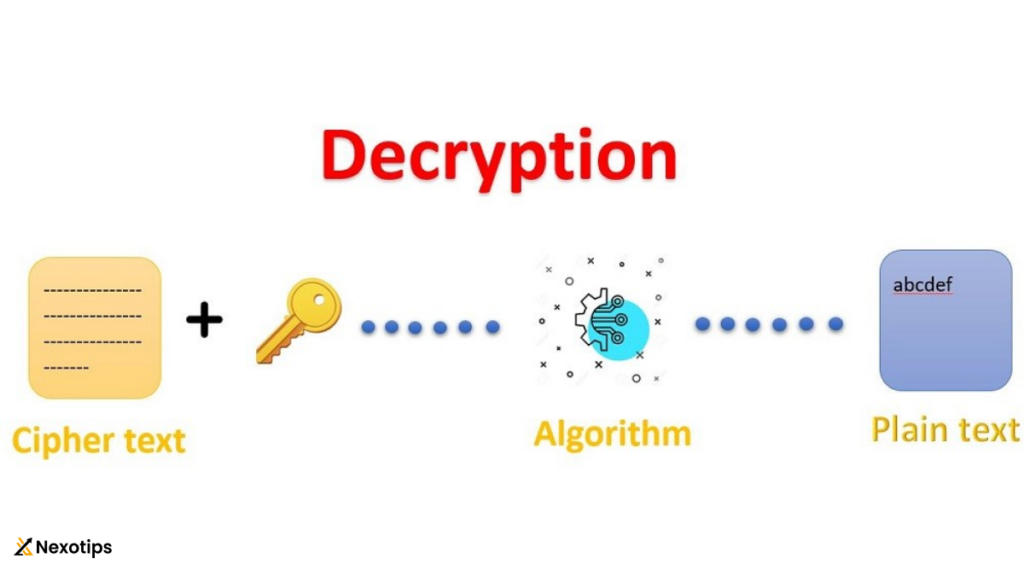
Key Management:

Effective key management is crucial for ensuring the security of encrypted data in cryptography . It involves generating, storing, sharing, and revoking cryptographic keys in a manner that minimizes the risk of unauthorized access. Key management protocols vary depending on the encryption scheme employed and the level of security required for cryptography .

Symmetric Encryption Algorithms:
Symmetric encryption calculations utilize a solitary key for both encryption and unscrambling. The cycle includes taking plaintext (comprehensible information) and changing over it into ciphertext (encoded information) utilizing an encryption calculation and a mystery key. This ciphertext can then be sent or put away safely. When the ciphertext should be decoded, the beneficiary purposes a similar key and an unscrambling calculation to change it back into plaintext.

High level Encryption Standard (AES):
AES is a symmetric encryption calculation broadly embraced as the norm for getting touchy data. It upholds key lengths of 128, 192, or 256 pieces and works on blocks of information, regularly 128 pieces in size. AES has been broadly broke down and investigated by cryptographers, and it is thought of as exceptionally secure against all known assaults when executed accurately.

Information Encryption Standard (DES) and Triple DES (3DES):
DES was one of the earliest symmetric encryption calculations generally utilized during the 1970s and 1980s. Notwithstanding, because of its moderately short key length (56 pieces), DES became vulnerable to savage power assaults as figuring power expanded. Triple DES (3DES) was acquainted as an upgrade with DES by applying the calculation multiple times with various keys. While 3DES gives further developed security over DES, it has to a great extent been supplanted by AES because of its more slow presentation and weakness to specific cryptographic assaults.

Uneven Encryption Algorithms:
Asymmetric encryption calculations, otherwise called public-key cryptography.

utilize a couple of keys:
a public key and a confidential key. These keys are numerically related, however getting the confidential key from the public key is computationally infeasible. The public key is shared transparently, permitting anybody to scramble messages expected for the proprietor of the key. The confidential key is kept mystery and is utilized to unscramble messages scrambled with the comparing public key.

RSA (Rivest-Shamir-Adleman):
RSA is one of the most broadly utilized awry encryption calculations. It depends on the trouble of calculating enormous indivisible numbers for its security. RSA can be utilized for encryption, advanced marks, and key trade conventions. The security of RSA depends on the viable trouble of calculating the result of two enormous indivisible numbers.

Elliptic Bend Cryptography (ECC):
ECC is a cutting edge uneven encryption calculation known for its effectiveness and solid security properties. It works on elliptic bends over limited fields and requires more modest key sizes contrasted with other awry calculations while giving identical security. ECC is especially appropriate for conditions with restricted computational assets, like cell phones and IoT gadgets.

Diffie-Hellman Key Trade:
Diffie-Hellman is a key understanding convention that permits two gatherings to lay out a common mystery key over a shaky correspondence channel. It is utilized in different cryptographic conventions, including SSL/TLS, SSH, and IPsec, to lay out secure correspondence channels. Diffie-Hellman doesn’t give validation or encryption all alone however shapes the reason for secure key trade in numerous cryptographic frameworks.

Hash Functions:
Cryptographic hash capabilities are numerical calculations that take an information (or message) and produce a fixed-size yield known as a hash worth or review. The critical properties of a cryptographic hash capability incorporate determinism (a similar info generally delivers a similar result), preimage obstruction (given a hash esteem, it is computationally infeasible to track down an info that hashes to that worth), second preimage opposition (given an info, it is computationally infeasible to track down an alternate info that hashes to a similar worth), and impact obstruction (finding two distinct data sources that hash to a similar value is computationally infeasible).

Secure Hash Calculation (SHA):
The SHA group of hash capabilities, including SHA-256 and SHA-3, are broadly utilized cryptographic hash capabilities normalized by the Public Foundation of Principles and Innovation (NIST). They produce hash upsides of fixed size (e.g., 256 pieces for SHA-256) and are generally utilized for computerized marks, secret phrase hashing, and information respectability check.

Message Condensation Calculation (MD5):
MD5 is a more established cryptographic hash capability that has been deplored because of weaknesses, for example, crash assaults. It delivers a 128-digit hash esteem and is not generally thought to be secure for cryptographic purposes. Be that as it may, MD5 is as yet utilized in specific applications where its security shortcomings are not a basic concern, like checksums for document honesty confirmation.

Computerized Signatures:
Digital marks give a method for checking the credibility and uprightness of advanced records and messages of cryptography . A computerized mark is made by applying a cryptographic calculation to a message utilizing the endorser’s confidential key. The beneficiary can then confirm the mark utilizing the underwriter’s public key. Advanced marks give non-renouncement, implying that the endorser can’t later deny marking the report.

RSA Computerized Mark Calculation (RSA-DSS): RSA can be utilized for advanced marks notwithstanding encryption. RSA marks serious areas of strength for give ensures and are broadly utilized in different applications, including electronic exchanges, programming conveyance, and report verification.

Computerized Mark Calculation (DSA):
DSA is a variation of the ElGamal signature plot and is determined in the Advanced Mark Standard (DSS) by NIST. It is regularly utilized in government and monetary applications and depends on the trouble of taking care of the discrete logarithm issue in a limited field.

Elliptic Bend Computerized Mark Calculation (ECDSA):
ECDSA is a computerized signature calculation in view of elliptic bend cryptography. It offers more modest key sizes contrasted with conventional RSA marks while giving comparable security. ECDSA is especially appropriate for conditions with restricted computational assets, like cell phones and IoT gadgets.

These cryptographic methods assume a critical part in getting computerized correspondences, safeguarding touchy data, and laying out trust in electronic exchanges. By understanding their fundamental standards and attributes, people and associations can arrive at informed conclusions about the determination and execution of cryptographic arrangements customized to their particular security prerequisites.

In an increasingly interconnected world, cryptography serves as the cornerstone of digital security, enabling secure communication, data integrity, and authentication. By mastering the essential concepts of cryptography, individuals and organizations can fortify their defenses against cyber threats and safeguard sensitive information effectively. As technology continues to evolve, staying abreast of the latest cryptographic techniques and best practices will be paramount in maintaining robust cybersecurity posture.